Skepticism emerges as a reaction wherever a certain, commonly held notion of truth begins to unravel. Operating with this notion of truth, we can try to slip out of the grasp of skepticism, but inevitably we trace the same maddening circle right back into its clutches. Can we model this worldview as a machine?

Factual Discourse Machines

The Classical Factual Discourse Machine

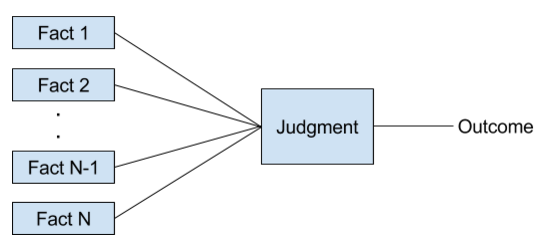
We take as our starting point the most naive view of factual discourse possible. All factual discourse involves acts of demonstration. I present the facts to support my conclusion, the more true facts I can present the closer I push you until you cross the threshold of agreement. This assumes that discourse works something like a machine, where the Classical Factual Discourse Machine might look something like the following (inputs and outputs are binary, true or false):

Following Aristotle, we might call the inputs our “premises” and the output the “consequence”. Since we have a machine here, we can also define this in code. Let’s construct a simple Ruby implementation:

class Judge
  attr_reader :min_required_facts, :assent_threshold

  def initialize(min_required_facts, assent_threshold)
    @min_required_facts = min_required_facts
    @assent_threshold = assent_threshold
  end
end

def judgment(judge, premises)
  return false if premises.size < judge.min_required_facts

  true_premises = premises.select(&:itself)
  percent_true = true_premises.size / premises.size.to_f

  percent_true >= judge.assent_threshold
end

Each individual judge has a certain bar for the minimum number of facts provided as evidence of an assertion, as well as a threshold for the percentage of facts that speak for that assertion. Once the minimum number of facts is presented and the threshold is breached, the judge will happily give his assent to the proposition in question. We can render a judgment on a statement supported by a given set of premises as follows:

aristotle = Judge.new(3, 0.51)
puts judgment(aristotle, [true, true, false, false, false]) # false

The above machine has the nice property of being easy to reason about, we keep presenting new facts and the weight of the facts eventually compels agreement.  The machine is also tunable, some individuals are more gullible some are more paranoid or pedantic. Each of these individuals could reasonably be modeled by this machine. In addition, while individual judgments may still vary, there is always the hope that at some point I can push you over the threshold and into agreement with me through factual demonstration. We also get a simple notion of truth – something is true if it has strong enough support from its premises. The classic, strong notion of truth can even be modeled here, namely by a judge with an assent_threshold of 1.0 – in other words, a judge who will only accept something if all the premises speak for it and none against it.

If all this seems a bit too simplistic that’s because it is. If we examine the premises closer, we see that we can always ask “What makes this premise true?” To answer this question our only recourse is to another round of demonstration and judgment, and any premises involved there could also be subject to the same scrutiny.

This observation – that not all premises are simple axioms – led Aristotle to distinguish between perfect and imperfect syllogisms:

“I call that a perfect syllogism which needs nothing other than what has been stated to make plain what necessarily follows; a syllogism is imperfect, if it needs either one or more propositions, which are indeed necessary consequences of the terms set down, but have not been expressly stated as premises”

– Aristotle, “Prior Analytics” (I.1.24b.23-26)

The Classical Factual Discourse Network

What even Aristotle knew is that this simple discursive machine isn’t enough, our premises have relationships to other syllogisms and their premises. In short, our knowledge forms a network or web of discursive machines, and this “imperfection” means we now have to account for two types of facts – simple and complex. A visual model of this network would look something like the following:

Similarly, we need to update our code model to account for this:

def ComplexPremise
  attr_reader :premises

  def initialize(premises)
    @premises = premises
  end
end

def judgment(evaluator, premises)
  return false if premises.size < evaluator.min_num_facts

  reduced_premises = premises.map do |premise|
    if premise.is_a? ComplexPremise
      judgment(evaluator, premise.premises)
    else
      premise
    end
  end

  true_premises = reduced_premises.select(&:itself)
  percent_true = true_premises.size / premises.size.to_f

  percent_true >= evaluator.assent_threshold
end

An example evaluation using this new machine would look as follows:

aristotle = Judge.new(3, 0.51)
puts judgment(aristotle, [true, ComplexPremise.new([true, false, true]), false]) # true

This new discursive machine is certainly a boon. We have all the nice features of the original and our notion of truth is preserved. As a bonus, we can now model relationships between factual premises.

However, we are quickly plagued by additional problems when we ask, “How do we distinguish a complex premise from a simple premise?”. This is the question concerning grounding.

Grounding

In philosophy, we give the name ground to those facts that represent a stopping place for this regression of discursive machines. In our own language we would say that simple premises represent grounds.

What gives a fact the status of a ground? What makes grounds unquestionable? If we should, say, try to recuperate the Figure 1 notion of truth from the Figure 2 factual discourse network, we will quickly despair at our inability to find any simple, general rule for doing so that doesn’t amount to handwaving. We cannot find a simple universal test for distinguishing grounds from unquestioned premises.

It is this despair at the futility of seeking permanent grounds that fuels the maddening circled traced by Wittgenstein’s “On Certainty”. Each time we think we have made progress, we exit the tunnel to find ourselves again confronted by the meaninglessness of “I know”. What ultimately evaporates for the reader is the notion that there is any purpose in seeking grounds that are both eternal (will last forever) and universal (apply equally everywhere). This desire for eternity and universality underlies the commonly held notion of truth – namely, that there are eternal and universal facts, and that we possess the ability to distinguish them from common prejudices.

An Alternative

To escape this vicious circle, what we can instead do is change the game. If our factual discourse really amounts to a kind of machine, then perhaps it is more fruitful to examine the effects that the introduction of different grounds have on the overall machine, and the effects this modified machine has on life itself. Rather than looking for the one true set of grounds, we could instead begin exploring the variety of possible grounds. So long as we understand that every grounding is contingent and provisional – that it comes with a shelf life, be it 50 seconds or 50 centuries – we are free to experiment here unencumbered by the notion that we are seeking eternal and universal truth, a notion we find continually frustrated by the vicious circle of skepticism.

Fresh air, freedom from the superfluous teleology of the commonly held notion of truth. In fact, we no longer believe in truth or certainty. This is the meaning of Nietzsche’s famous “Gott ist tot” (“God is dead”). This does not mean that we can never know the means for accomplishing our desired ends, just that we cannot know these means to be eternal or universal, that there is no transcendent mechanism that gives us the leverage to make such claims.

Exercises

1. Suppose that we decided to model truth as Bayesian rather than Boolean, that is as a real-numbered probability value in the range [0, 1] rather than as a binary value in [true, false]. Write an updated judgment function to handle Bayesian truth probabilities. What are some implications of this Bayesian model for the concept of eternal and universal truth?